皆さんこんにちは。
前回は時系列情報を含む水質データに対して標準化・四分位範囲を使ったスケーリングを行いましたね！
ですが、依然として外れ値が含まれている為そのまま機械学習に使う事はできませんでした💧

そこで、今日は元の水質データを加工してから機械学習を行ってみたいと思います。
使うデータは某ダムの2018年5月～10月下旬の水質データ。
前回と同じデータです。
気泡循環の解析の為に用意した加工済みデータですが、機械学習ではなるべくきれいなデータを使いたいのでこちらを使用します。
(事前にファイルのバイト数が十分にあるデータのみ選択し、可能な範囲で欠測を補間、水深0ｍ～15ｍ部分をカットしています。)
スケーリングの回では省略していましたが、グラフで表すとこんな感じです↓

グラフを確認するとPCY、pH、Chlaは全層に渡ってバンドが濃く出ている箇所が確認出来ます。DOも10月20日頃に白いバンドが出てますね。
いきなり値が変わっている箇所はおそらくエラー値なので、これらの項目は機械学習には使いません(笑)　※エラー除去する処理が手間なので･･･。

今回は一番安定している水温を使って、ロジスティクス回帰による分類を行いたいと思います。
少々省きましたがここまでがいわゆる「データクリーニング」に当たります。

---

次はデータ整形です。

【training.csv】

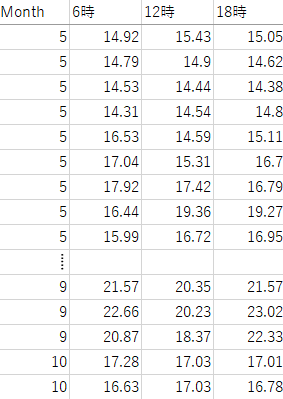
機械学習可能な形にデータを整形します。
水深軸、時間軸のあるデータのままでは扱いづらいので、表層から水深50cm地点でかつ、6時、12時、18時の水温データを抽出します。
定点のデータを抽出することで水温の外れ値を完全に除去しています。
これらを説明変数として、何月か？というのを目的変数とします。

このように目的に応じてデータ整形を行う事で、“水深50cm地点のある時刻の水温から何月のデータか予測する”ことが可能です。

今回使用するロジスティクス回帰という手法についてですが、ロジスティクス回帰とは統計手法の回帰分析の一つで、直線yの式で表される線形モデルと言えばピンとくる人が多いのではないでしょうか(^^)

ここでは、いくつかの説明変数(特徴数)から目的変数を予測するものです。
基本的に、目的変数はYes/No、または0か1か等の2値で判別できるもので、どちらに分類されるかの確率を予測します。
今回の使用するデータは目的変数が5月、6月、7月、8月、9月、10月の合計6個なので、本来はマルチクラス分類に適した別のモデルを使用するのが好ましいですが、LogisticRegressionにもマルチクラスに拡張する機能が付いているため、このまま進めます。

---

機械学習を使った予測は以下の短いコードで完結します。

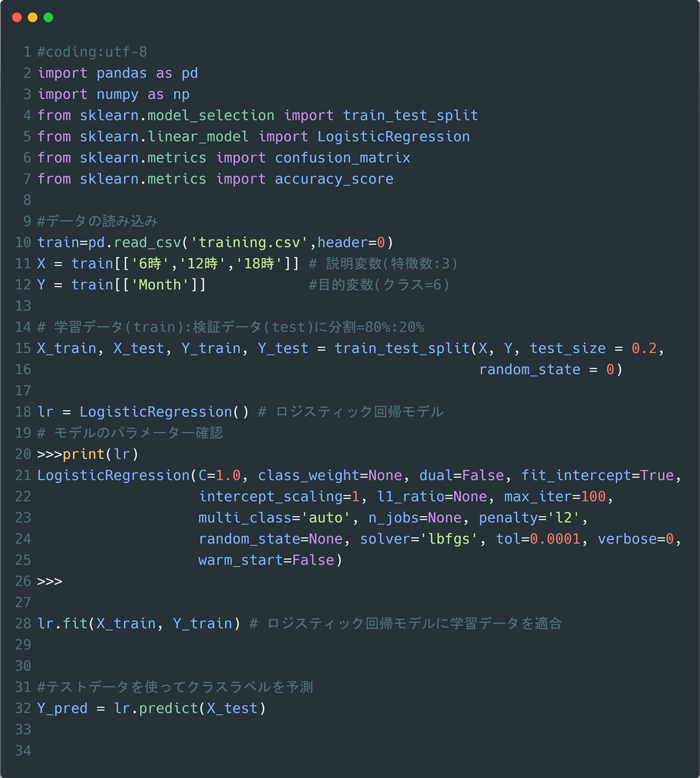
流れをまとめると、

1 データの用意
2 ①を説明変数と目的変数に分割
3 ②を学習用データとテスト用データに分割
4 学習用データをモデルにフィッティング
5 学習済みのモデルでテストデータを予測

とてもシンプルですね。データの用意の方が大変です(笑)


また、今回予測に使用したモデルのパラメーターは以下です。

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, l1_ratio=None, max_iter=100,
multi_class='auto', n_jobs=None, penalty='l2',
random_state=None, solver='lbfgs', tol=0.0001,
verbose=0, warm_start=False)

このように沢山のパラメーターがありますが、中でもsolverというパラメーターがこのモデルの核で、使用するアルゴリズムを指しています。ここでは'lbfgs'。準Newton法(L-BFGS)が選択されています。
L-BFGSに関してどのような計算をしているのか調べると、どうやら初期推定値から最適な推定値になるまで反復計算をするようです。こういった特徴から「機械学習」と呼ばれているのが納得できますね💡

通常各パラメーターは使用するデータ毎にチューニングが必要ですが、今回チューニングは行わず、デフォルト値で学習します。なぜならモトハシもチューニングに関してはまだ理解が追いついていませんので💧

---

次いで、サイキット・ラーンの公式に
『マルチクラス問題の場合は「newton-cg」、「sag」、「saga」、および「lbfgs」のみが多項損失を処理します。』と記載があることから、L-BFGSは用意した学習データ(6クラス分類)に適したアルゴリズムだと考えます。

また、他項損失とはモデルの予測精度を評価する損失関数のことで、予測値と実際の値のズレを表してくれます。
損失関数の値が小さければより正確なモデルと言え、LogisticRegressionにおいて使用するデータが他項(＝マルチクラス)に分類される場合はこの計算が厳しくなるようです。


以上を踏まえて予測結果と予測精度を確認してみましょう(^_^)v

学習データの精度は81％でまあまあってところですね💡
一方テストデータは58％とかなり低めです。
(ちなみに、標準化したデータを学習させると学習データ77％・テストデータ63％の精度になりました。
あんまり変わりませんね💧)

最後にresultにテストデータの値と実際の月、予測結果をまとめてみました。
確認すると、テストデータ19個のうち正解が11個なので11/19=0.5789.. 予測精度とは正解率のようですね。
(マルチクラスに対応していないアルゴリズムを使用すると、損失関数がうまく機能せず、この正解率が狂うのでしょうかね･･･？？また時間のあるときに確認してみようかな）

予測値と実際の値の誤差については、例えば5月と6月、6月と7月、5月と10月などで間違った予測をしていますね！
この原因として、training.csvを作成する際に、例えば5月のデータなら1日～31日までの6時、12時、18時のデータをすべて5月のラベルにしてしまっている為、前後の月との明確な特徴が現れていないデータを学習し、テストデータを評価してしまったと考察しています。
5月31日と6月1日なんて大して気候に違いなんて無いですからね(笑)
5月と10月を間違えているのは、単純に定時刻の水温マップが似ていたからでしょう。
まとめとしては、水温だけだと流石に正確な月の予測までは難しいようでした(；´Д｀)


と、まあ今回は以上です。
機械学習自体は簡単にできるので、質の良い学習データを用意する事と適したモデルの選択、パラメーターの調整が重要だということが何とな～く分かって頂けたのではないでしょうか♬