皆様こんにちは！
新年からしばらく探索アルゴリズムについて取り上げましたが、今回紹介する「ハッシュ法」は導入の部分をお話して最後にしようと思います。

私自身調べていると「探索アルゴリズム」は情報系の試験にも出題されているようですね！
この試験でも大抵ハッシュ関数は実際のアルゴリズムからmodなど四則演算に置き換わっていることからかなり難易度が高いものと思われます。
最近SNSなどでよく「#」ハッシュダグを利用するケースが増えていますが、この“ハッシュ(#)“とハッシュ法は意味が異なるようです。

ちなみにモトハシこのハッシュ法が気になって基本情報技術者試験と、情報処理安全確保支援士のテキストを確認しましたが、後者のテキストには実際のアルゴリズムに関して簡単に記載がありました。
興味のある方はテキストを手にとってみるか、ネットで調べても情報は上がってくるので参考までに。

---

さて、本題に入りますね。
前述のように実際に現場で使用されているハッシュ法はかなり高度な計算のようで、Pythonでも有名なハッシュ関数(MD5、SHA224等‥)はhashlibでライブラリとして提供されています。

例としてMD5(Message Digest 5)というアルゴリズムは任意の文字を128bitに変換するハッシュ関数の1つであり、bitとはコンピューター上の最小単位を表しています。
8bit=1byte　であり、bitとは2進法(2を底にして)の1桁で表されます。
(byteは使用環境によってビット数が変わります)
MD5のアルゴリズムでは入力データのパディングを行うらしいのですが、初見では何をしているか分かりません(笑)

そこで、bitや2進法について理解を深めたいと思います。
例えば、ひらがなの「あ」はUnicode番号がU+3042(HTMLコードでは12354) です。
Unicode番号とは文字に割り当てられた世界共通の番号で、この値は検索すると出てきますし、Python標準モジュールでも確認することができます。

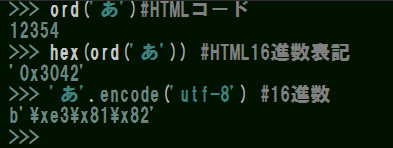
モジュールのord()はその文字のUnicodeコードポイントを整数で返し、hex()は入力された整数から16進数に変換した文字列を返します。
6進数に変換された値の先頭に付いている「0x」は16進数であることの目印で添字のようなものです。
ここでutf-8≠Unicodeであることに注意してください。
utf-8はあくまでUnicodeで識別されたコードポイント(文字に割り振られた識別番号)を別の16進数数値に変換する方法で、独自の変換ルールを持っています。
そのため上図で「あ」をutf-8に変換したとき、符号混じりの「e38182」というUnicode番号とは全く別の数値になります。

utf-8の他にもShift_Jisなど多数存在する文字コードは、符号化方式(URLエンコード) と言って、文字列をバイト数に変換する方式の1つであり、その方式のルールに従って「3042」→「e38182」など、コードポイントが決定します。
これはUnicodeで対応付けされたコードポイントを、実際にコンピューターで利用できる形に変換するメソッドです。


以下参考として「あ」を2進数で表した時の数値を載せました。
PCのメモ帳の文字コードはUtf-8なので試しに「あ」を入力してプロパティを確認してみてください。3byteなはずです。

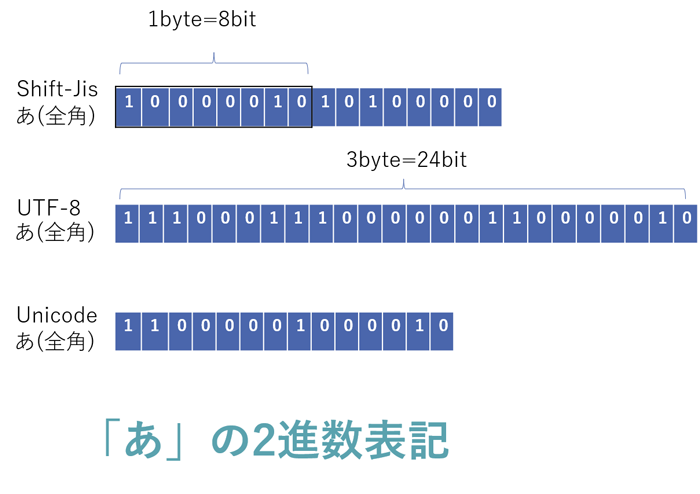
同じ文字でも文字コードが違うと数値化した結果が別物になるなんてややこしいですが、このような変換ルール(≒ハッシュ関数の考え方)で、結果として得られた数値を利用して識別や探索を行うのが平たく言うハッシュ法です。

とは言っても、エンコードの変換ルールを説明するのはナンセンス😨
もっと一般的な計算のベースとなっている部分に焦点を当てたいので、モトハシは考えました。
例として先程挙げた「あ」について、Unicode のHTMLコード「12354」は一般的な10進数表記(10で桁が上がる表記)のようなのでこれを元に計算を確認しましょう。

【10進数(整数)→16進数への変換】

まず「12354」数値を16で割って16進数に変換してみます。
変換方法については調べれば情報が出てくるので割愛しますが、私が大学時代の講義では公約数を求めるときのように連除法を使い、除算で出た全ての余りを、計算順序とは逆に並べて変換を行っていました。
(ちなみに当時この講義の単位を落としています…😲 (不安でしか無い))

① 12354÷16＝772…2 (1回目の割り算)
② 772÷16＝48…4 (2回目の割り算)
③ 48÷16＝3…0　　　 (3回目の割り算)
④ 3÷16＝0…3　　 　(4回目の割り算)

2回目以降の割り算は1つ前の計算で得た商を割られる数にして再度計算します。
これを商が0になるまで繰り返し、最後に結果を④→①、商から先頭に並べると「3042」となります。
つまりこれがUnicode番号(＝12354)で、この16進数表示の番号は文字コードの世界基準です。

【16進数→10進数(整数)への変換】

そして16進数「3042」から10進数に変換する際は、
(3×163)+(0×162)+(4×161)+(2×160)＝12288+0+64+2
＝12354

このように3042の各桁に基数(16倍ごとに桁が増えるというルール)を掛けた総和が10進数表記となります。
ここで基数は別名重みとも呼ばれますが、DeepLeaningのニューラルネットにも重みという概念がありますね。
一見別物のようであっても入力されたデータをあるルールに基づいて変化するという考え方は同じであることがよくわかります。

【16進数→2進数(bit)への変換】

同じように16進数「3042」から2進数に変換する場合、16進数の数え方は0～9までは10進数と同じで、その後はA～Fのアルファベットで表されます。
また16進数表記の1桁は2進数表記の4桁分に相当する決まりがあるので、「3」「0」「4」「2」の1桁ごとに先程と同じく①～④の計算を行い、商と余りを出します。

イ) 3÷2で連除法 ＝1…1、1÷2＝0…1 　　　　　　(1桁目3の割り算)
ロ) 0÷2で連除法＝0…0　 　 　　(2桁目0の割り算)
ハ) 4÷2で連除法＝2…0、2÷2＝1…0 、1÷2＝0…1 　(3桁目4の割り算)
ニ) 2÷2で連除法＝1…0、1÷2＝0…1 　　　 (4桁目2の割り算)

この結果を並べると「11 0 100 10」となります。
ここでは16進数の1文字は4bitに相当するので、2桁目以降、連除法の余りの総数が4桁未満なら左側を0パディングした値「11000001000010」が答えとなります。

Utf-8の16進数表記「e38182」も同じように2進数に変換することができます。


今紹介した計算、特に2進数への変換がハッシュ関数のベースとなっている考え方ですが、現実のハッシュ法は情報セキュリティで使用されることもあり、ハッシュ値(計算結果)から元の値を逆算が難しい点や、入力文字の長さが足りない場合でも一定の長さのハッシュ値を排出する処理が必要な点などから計算の複雑さが容易に想像できます。
アメリカの国家安全保障局(NSA)によって開発されたハッシュ関数のアルゴリズム「SHA256」に関してはその計算プロセスがWEB公開されているので、詳しく勉強したい人は検索してみてください♪
いや～、単位落としたくせにここまで書けたらモトハシ的には上出来です(笑)
長くなりましたが今日はここまで($・・)/~~~