皆さんこんにちは、今日は前回に引き続き探索アルゴリズムの二分探索法をPythonでコーディングした例をご紹介します🤓
クレームが来ないよう最初に言っておきたいのですが(笑)……
“ソート済みの配列の中央値を基準に2つに分け、目的の値がそのどちらのグループに所属するのかで繰り返し探索を行う“という二分探索の基本原理は図や文章など既に様々なページで説明されています。
しかし、これをプログラムで組み立てた時、人によっては記述方式が微妙に変化したり、プログラミングのルールと相まって表現がややこしいので、なるべくポイントを噛み砕いてお話しようと思います。
そして多分モトハシが組み立てた以外にも色々な記述方法があるはずです。

ではコード全体を示します。

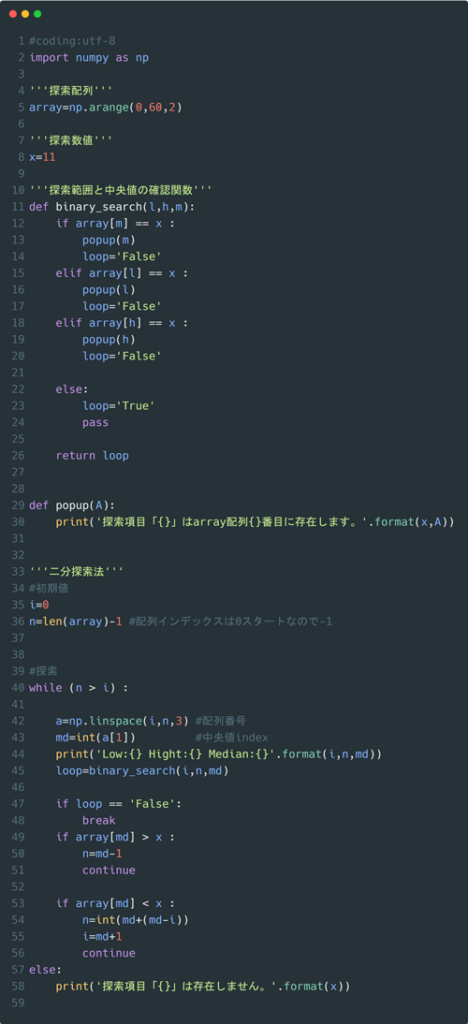
まず、前提ですが二分探索の計算量はlog2(n)回です。(※log2(n)のｎは配列の個数です。
プログラム上の変数ｎは探索範囲の終点を意味します。)

今回探索に用意した配列arrayは0～58まで合計30個あるので、

大計算量は約5回となりますが、本プログラムコードでは5回目の探索で反復条件を満たさなくなり、探索が終了します。↑


このように計算量が予め分かっていれば繰り返し構文はfor を使って記述できそうですが、配列の中身が日付とか数値以外のものでもプログラムが機能するように、また1回の探索で必ず条件分岐と探索範囲の確認を行う必要があることからコード40～58行目の探索はwhile構文で記述しました。
詳しい理由については後に記載しています。

---

以下の図は、プログラムコードと同じく探索目標を「11」、変数iを探索範囲の開始点、nは探索範囲の終点として、ｎ＞iが成り立つ間反復処理を行う工程を表しています。

二分探索のアルゴリズムは配列の中央点の値を境として左右どちらに目標値が存在するかを探索します。
最初は配列の左側を先頭として0，1，2・・・29個(合計30個)それぞれ数値の入ったボックスが並んでおり、その中央点は黄色で塗り分けをしています。
中央点は配列番号の最初と最後を足して2で割るか、先頭から順番に数えてちょうど真ん中にくる値が中央点です。
今回のように配列個数が偶数であれば中央点が2つになるので、その２つの平均を取っても構いません。

このプログラムでは初期配列の終点から始点方向(29→0)へ反復回数が増えるごとに探索範囲が半減していき、(mdに格納された値)＜(探索目標値)　となった時点で探索範囲が昇(0→29)方向に反転するようになっています。
この“何回目かで探索範囲が反転する”という特徴を持っていることが、なぜプログラム上で繰り返しをWhile構文で書いているかの理由にもなります。

もしかすると例外的な使い方もあるのかもしれませんが、私が知る限りfor構文は線形探索のように回数が決まっている場合に使用することが多く、<さらに(終点→始点)もしくは(始点→終点)の一方通行で反復処理を行うイメージです。
何回目の探索で目標を見つけられるか未知で、反復の時々で範囲が進んだり戻ったり変動する場合、for構文での記述は不向きであり(というか逆に難しいので)、今回のようにWhile構文を使用します。

また初期配列個数が奇数の場合は1つの中央点に対して両サイドの配列個数は等しくなりますが、今回のように偶数の場合、中央点mdは小数となり、これをint型の整数に修正することで探索範囲が(md-i)分反転した際インデックスのズレが生じます。
工程図では最後6番目の「10」が切り捨てられていますよね？
このズレによる探索エラーを防ぐためと、探索項目が存在しない場合の無限ループを回避するためbinary_search関数で探索範囲の始点、中央点、終点を毎回確認させています。
popup関数は探索目標が見つかった時と見つからない時で繰り返し探索を継続するか否か決定する関数です。


そして、コード全体を実行するとこのような結果が表示されます。

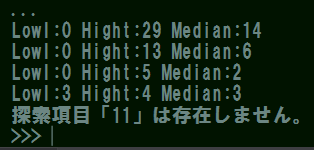
Low,Hight,Medianは毎回の探索範囲を表示しており、すべて初期配列から数えた配列のインデックス番号(i,n,md)です。
無事二分探索の実行ができましたね♪

では今日はここまでにします。