皆さんこんにちは。

最近、朝夕は大分過ごしやすくなりましたね。

今日はいつもより少し踏み込んで、

異常検知という枠組みから、既に多くの文献で述べられているような、本質的な話をしようと思います。

私が知る限り、水質センサーデータの異常値をはじめ、予測したい水質変化や捉えたいイベントの殆どは特徴項目同士の相互関係と時系列に起因します。

そこで、水質のように相互に影響しあう項目を統合し、水質状態や異常を判断する方法について、

入社間もないころから変化量、局所密度、K-means、SVM等を検証し、そのたびに研究会で意見交換を行ってきました。

しかし、未だにデータチェックは手作業というのが現実です。

今回は、水質のような環境科学分野に限って、手っ取り早く使えそうなツールが存在しない理由と課題について、異常検知モデルのVRAEを使って深堀してみました。

使用する水質データ

以下のコンターは国内某ダムの2025年5月のデータです。

概ね綺麗に計測できていますが、5/28以降センサー交換による感度誤差があります。

感度誤差が発生した場合、普段手作業によって修正しているため、この期間を異常としてモデルが捉えることを期待します。

ポイント1：センサー感度が変わっても深さ方向のパターン(躍層状態)は維持している

ポイント2：コンター図ではデータ密度の関係で目視不可能なエラー値が含まれている

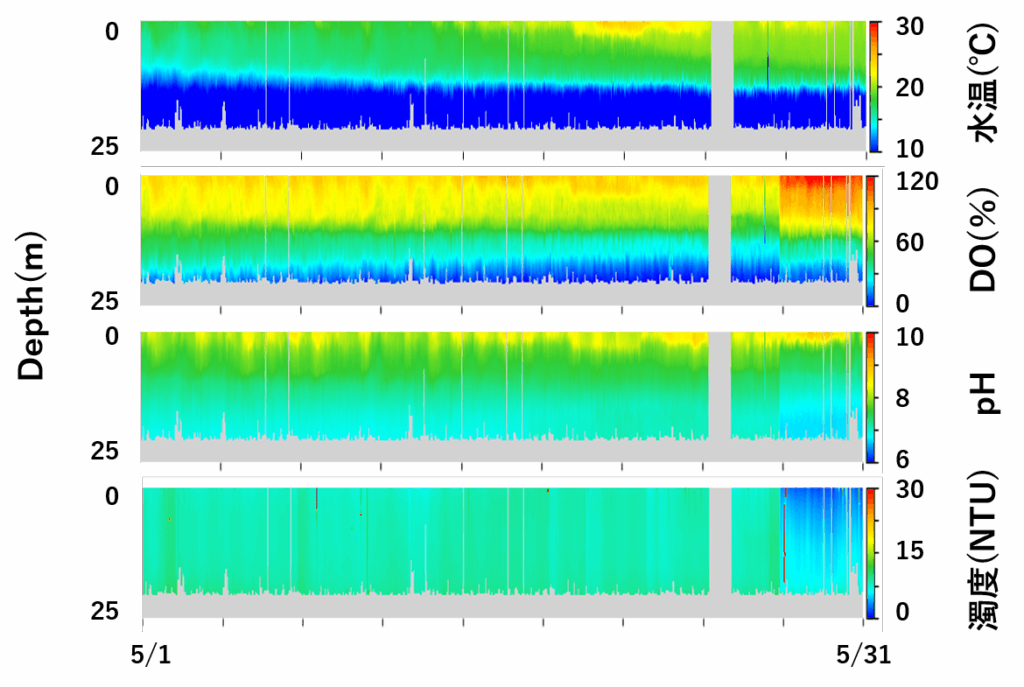
特徴次元を簡略化するため今回は表層の時系列データを使用。　shape:(1016, 4)

時系列を図化すると、コンターでは確認できなかったスパイクが見られ、
感覚的に水温、DO%、濁度の変化が目立ちます。

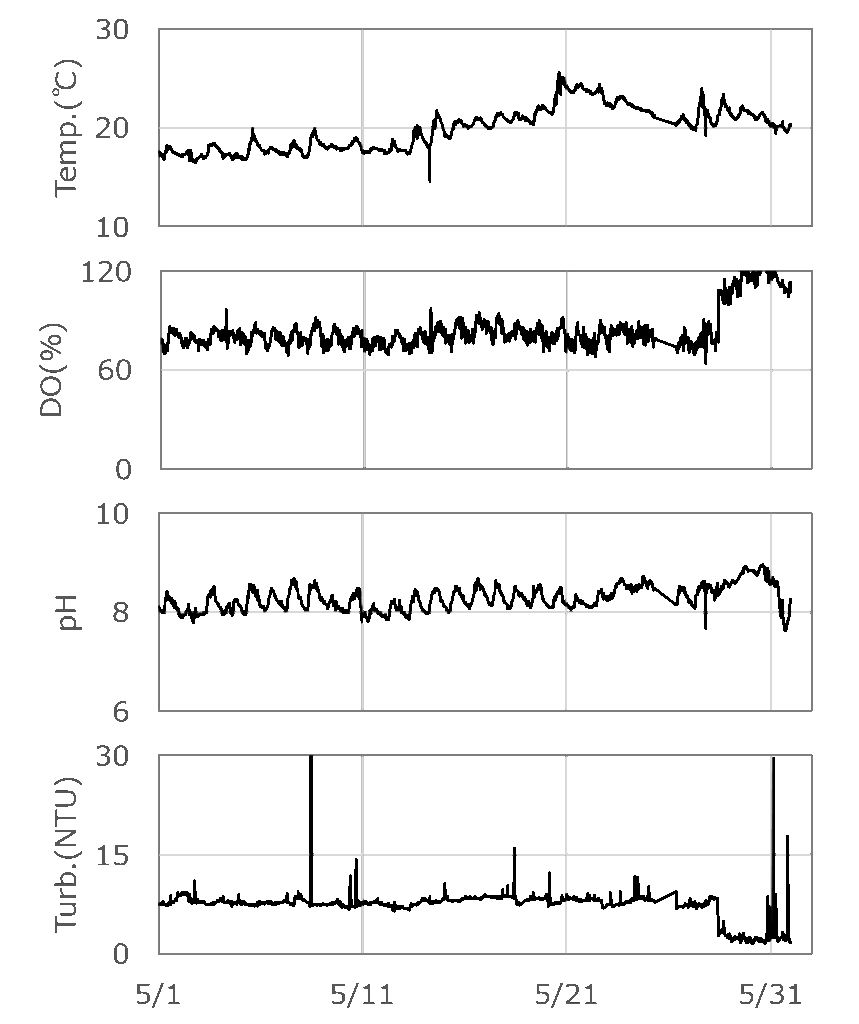
モデルに入力するデータの形状は、Otto Fabius, Joost R. van Amersfoort（2014）に記述されている手法を再現します。

具体的には、一連の時系列を一定区間に区切る場合（オーバーラップなし）と、時系列の繋がりを明確にした場合(オーバーラップあり)の2通りのデータセットを用意します。

オーバーラップなし：2025年5月の表層水質データ（水温、DO%、pH、濁度）を8バッチ127個に分けてモデルへ入力

オーバーラップあり：2025年5月の表層水質データ（水温、DO%、pH、濁度）を前後のバッチで50％重複するように分けてモデルへ入力

作業はおおまかに 情報圧縮→再構成→スコア生成　といった流れです。

コード全文

import torch
import torch.nn as nn
import torch.nn.functional as F
import pandas as pd
import numpy as np

class VRAE(nn.Module):
    def __init__(self, input_size, hidden_size, latent_size, sequence_length):
        super(VRAE, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.latent_size = latent_size
        self.sequence_length = sequence_length

        # Encoder
        self.encoder_lstm = nn.LSTM(input_size, hidden_size, batch_first=True)
        self.fc_mu = nn.Linear(hidden_size, latent_size)
        self.fc_logvar = nn.Linear(hidden_size, latent_size)

        # Decoder
        self.decoder_input = nn.Linear(latent_size, hidden_size)
        self.decoder_lstm = nn.LSTM(hidden_size, hidden_size, batch_first=True)
        self.output_layer = nn.Linear(hidden_size, input_size)

    def encode(self, x):
        _, (h_n, _) = self.encoder_lstm(x)
        h_n = h_n.squeeze(0)
        mu = self.fc_mu(h_n)
        logvar = self.fc_logvar(h_n)
        return mu, logvar

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mu + eps * std

    def decode(self, z):
        h_dec = self.decoder_input(z).unsqueeze(1).repeat(1, self.sequence_length, 1)
        out, _ = self.decoder_lstm(h_dec)
        return self.output_layer(out)

    def forward(self, x):
        mu, logvar = self.encode(x)
        z = self.reparameterize(mu, logvar)
        x_recon = self.decode(z)
        return x_recon, mu, logvar

def loss_function(x_recon, x, mu, logvar):
    recon_loss = F.mse_loss(x_recon, x, reduction='mean')
    kl_loss = -0.5 * torch.mean(1 + logvar - mu.pow(2) - logvar.exp())
    return recon_loss + kl_loss

def mean_norm(df_input):
    return df_input.apply(lambda x: (x-x.mean())/ x.std(), axis=1)

def create_overlapping_batches(data_np, window_size=127, stride=64):
    data = torch.tensor(data_np, dtype=torch.float32)
    batches = []
    for start in range(0, data.shape[0] - window_size + 1, stride):
        batch = data[start:start + window_size]
        batches.append(batch)
    return torch.stack(batches)  # shape: (num_batches, window_size, features)


# Dataset preprocessing
df=pd.read_csv('mytest.csv',usecols=(2,3,4,5),header=0,index_col=None)
stdf=mean_norm(df)　♯ standardization

# ①タイムステップ重複なし
x_batch=stdf.values.reshape(8,127,4)

# ②50％重複あり
x_batch=create_overlapping_batches(stdf.values, window_size=127, stride=64)

# 学習
model = VRAE(input_size=4, hidden_size=64, latent_size=20, sequence_length=127)
reconstructed, mu, logvar = model(x_batch)  # input: shape (batch, time, features)
loss = loss_function(reconstructed, x_batch, mu, logvar)
loss.backward()

#再構成誤差（MSEベース）
reconstruction_error = torch.mean((x_batch - reconstructed)**2, dim=(1,2)) # shape: (batch,)

# KL距離（VAEの定義に基づく）
kl_div = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp(), dim=1)  # shape: (batch,)

# 統合スコア（α・βの重みはチューニング可能）
alpha = 0.7 # センサー値(パターン変化・スパイク・欠測)に対する誤差感度
beta = 0.3  # 各バッチ構造の違和感に対する感度(KL Divergence：連続確率分布) 
anomaly_score = alpha * reconstruction_error + beta * kl_div  # shape: (batch,)
anomaly_score

スコアの解釈

再構成誤差

モデルが学習した時系列変動パターンとの誤差

⇒センサー値にパターン変化・スパイク・欠測があれば誤差が大きくなる

KL距離（KL Divergence）

各バッチ情報を圧縮し、正規分布へ近似させた空間上の分布（潜在分布）と理想的な正規分布との距離を測っている(ここでは連続確率分布を指す) 。※潜在空間は「KL距離によって定義される」のではなく、エンコーダによって構築され、圧縮→正規分布へ近似させるため情報量と表現の制約が掛かる。

⇒潜在分布に偏りがあったり、ヒストグラムがいびつであれば、指標が大きくなる。各バッチの構造的な違和感を捉える。

KL項の補足

Carl Doersch(2016)によると、多次元正規分布\(\quad\) \(q=N(\mu,\Sigma)\quadと\quad p=N(0,I)\quad\)のKL項は

\[{D}_{KL}(q \parallel p)=\frac{1}{2}(tr(\Sigma)+\mu^T\mu-k-\log det\Sigma)\tag{1}\]

このとき\(\quad\) \(k=潜在分布の次元数\), \(\quad\) \(tr(\Sigma)=\displaystyle \sum_{i=1}^k {\sigma}_i^2\),\(\quad\) \(\mu^T\mu=\| \mu \|^2\),　\(\quad\) \(\log det\Sigma=\displaystyle \sum_{i=1}^k \log{\sigma}_i^2\)

(1)を整理すると次式で表せる

\[-0.5\cdot(1+\log\sigma^2-\mu^2-\sigma^2)=\frac{1}{2}(\mu^2+\sigma^2-1-\log\sigma^2) \tag{2}\]

結果

結果：①オーバーラップなし

>>> x_batch.shape
torch.Size([8, 127, 4])

>>> anomaly_score
tensor([0.4858, 0.5354, 0.5567, 0.4629, 0.5297, 0.5051, 0.5262, 0.4741],
       grad_fn=<AddBackward0>)

>>> #recon_ratio
... reconstruction_error / anomaly_score
tensor([1.3355, 1.3441, 1.3469, 1.3303, 1.3424, 1.3379, 1.3418, 1.3333],
       grad_fn=<DivBackward0>)

>>> #kl_ratio
... kl_div / anomaly_score
tensor([0.2172, 0.1972, 0.1906, 0.2293, 0.2012, 0.2117, 0.2025, 0.2222],
       grad_fn=<DivBackward0>)
>>> 

３番目のバッチが最も高いスコア（0.5567）を示したことから、5/8～5/12の濁度スパイクに最も反応したと推測できる。

センサーが切り替わる5/28以降のデータは８個目のバッジにあたるが、スコア事態は２番目に低い値をとっている。

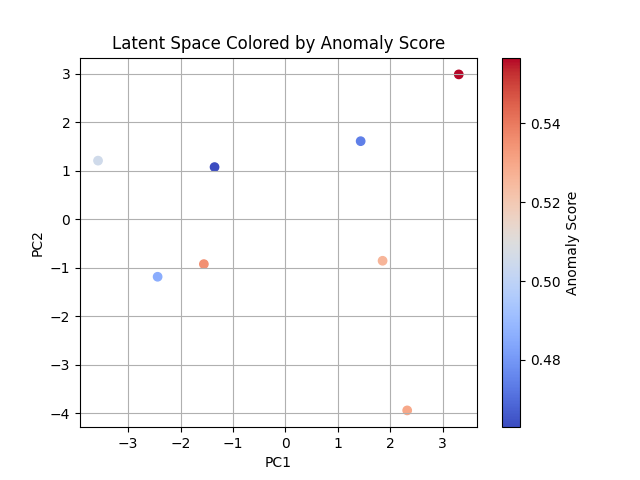
↑オーバーラップありの潜在分布を２つの特徴（PC1・PC2）でマッピングし、スコアを付与した図

結果：②オーバーラップあり（タイムステップ 50％重複あり）

>>> x_batch.shape
torch.Size([14, 127, 4])

>>> anomaly_score
tensor([0.5456, 0.6309, 0.5073, 0.5114, 0.5357, 0.6010, 0.6658, 0.7514, 0.6906,
        0.6249, 0.5329, 0.5289, 0.6670, 0.5387], grad_fn=<AddBackward0>)
>>> #recon_ratio
... reconstruction_error / anomaly_score
tensor([1.3380, 1.3502, 1.3311, 1.3320, 1.3365, 1.3465, 1.3546, 1.3631, 1.3574,
        1.3501, 1.3364, 1.3355, 1.3547, 1.3366], grad_fn=<DivBackward0>)
>>> #kl_ratio
... kl_div / anomaly_score
tensor([0.2113, 0.1828, 0.2275, 0.2253, 0.2149, 0.1914, 0.1726, 0.1528, 0.1661,
        0.1831, 0.2151, 0.2172, 0.1723, 0.2146], grad_fn=<DivBackward0>)
>>> 

８番目のバッチが最も高いスコア（0.7514）を示したことから、5/14～5/17の水温・DO%のスパイクを含む範囲を異常と判断した事が伺える。

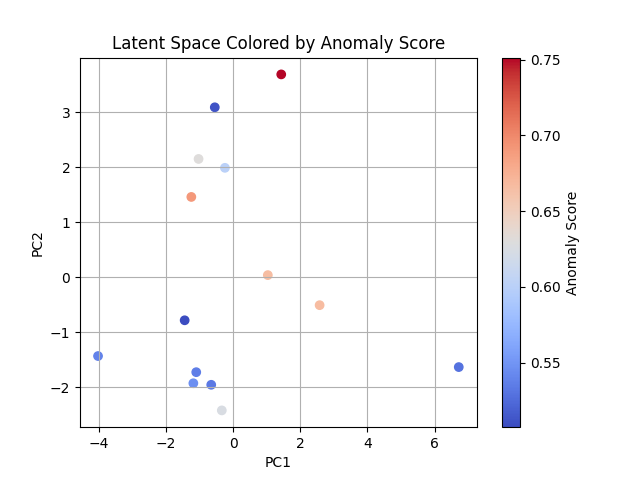
↑オーバーラップなしの潜在分布を２つの特徴（PC1・PC2）でマッピングし、スコアを付与した図

2つのデータセットのスコアから読み取れる事は、モデルはとにかく大小のスパイクに反応しているという点です。

また、潜在空間分布とスコアの図を見ると分かるように、潜在分布そのものがスコアに結びついているわけではない事が伺えます。

一見異常とは思えないような点にやや高いスコアが振られていたり、

明らかに逸脱している点のスコアが低かったりと、

これは本来検知したい現象と物理モデルの認識にズレがある事を示しています。

モデルは予測しやすい状態を正常とみなし、予測が難しい状態を異常とみなしますが、

予測が難しい＝水理・物理現象としての異常 とは限りません。

⇒潜在空間上で明らかに他と逸脱した点があっても、異常スコアは正常な場合がある

⇒理想的な正規分布から外れても、モデルが予測しやすいと判断すれば異常スコアは低くなる。逆もしかり。

また、統合スコアを出す際の再構成誤差とKL距離の感度（α・β）を逆転させたとしても、結果はそう変わりませんでした。

つまり、今回の検証で「潜在空間の分布と異常スコアの意味は一致しない」という結果が示せました。

これはVRAEモデルに限らず、モデル・レイヤーそのものの構造的な制約が、

「予測の容易さ」又は「予測困難性」にバイアスをかけている事を示しており、

最終的にモデルスコアと現象のギャップを生むと考えられます。

分かりやすく言うと、ほとんどの時系列予測では、圧縮した情報をもとの次元・形状に再構成する過程で線形レイヤーを使用しますが、
その過程で物理的に意味のある予測値に変換する役割を担っています。ただし、その予測が実際の現象と一致するかは別物で、
モトハシ的には他のLSTMモデルでも根本は同じと考えています。
※もし私の理解に誤りがあればご指摘ください。

最後に、

水質データの異常検知はかなり高難易度で、一朝一夕にはいかない話ですが、

既に異常検知モデルの社会実装に成功している業界は幅広いです。

そういった例と水質を比較すると、

データの質や構造、背景が根本的に異なるため、当然モデルスコアと現象のギャップの出方にも違いが生じます。

今後の取り組みとしては、以前から機械学習分野で議論されている通り、「意味」をモデルから引き出すための設計と工夫が必要だと感じました。

参考文献

Otto Fabius & Joost R. van Amersfoort（2014）：”VARIATIONAL RECURRENT AUTO-ENCODERS ”, arXiv:1412.6581 [stat.ML]

Jonathon Shlens（2014）：”Notes on Kullback-Leibler Divergence and Likelihood”,arXiv:1404.2000 [cs.IT]

Carl Doersch（2016）：”Tutorial on Variational Autoencoders”, arXiv:1606.05908 [stat.ML]

Mononito Goswami, Cristian Challu, Laurent Callot, Lenon Minorics, Andrey Kan（2022）：”Unsupervised Model Selection for Time-series Anomaly Detection”, arXiv:2210.01078 [cs.LG]