暑い日が続いてますが皆さんいかがお過ごしでしょう？

あっという間に今年も半分が終わって、そういえばもうすぐ夏休みですね🌻

この時期フェスやお祭り、プールなど野外イベント盛りだくさんですが、

モトハシはどちらかというと涼しいコテージでBBQや昼寝をしながら家族でのんびり過ごしたい気分です。

さて、

今日の話題はデータ整理とモデルの組み立てを行っていた時のお話です。

正直、自分の中で内容がまとまっていないので、私の個人的な意見・感想として受け取ってください（o_ _)ｏ））

データ特徴と整理の具体例

---

例えば、皆さんがアイスクリーム店舗の経営を任されたとして、

人件費・在庫・発注・売り上げなどの管理を行っているとしましょう。

この場合、アイスクリームということで

１日の売り上げに直結するのは概ね気温（天気）と時間帯ですが、

一週間の売り上げは追加要素として雨量や曜日が関係し、

中長期の売り上げは気温の他、従業員の対応・アイスクリームの品質なども関係してくると思われます。

（中長期となるとアンケート調査や調理者の記録、材料一つ一つの詳細データが必要になりそうですね）

上記のデータが与えられたとき、全期間で気温との関りが強いことから、

一般的な売り上げ予測では真っ先に線形回帰が用いられる問題ですが、

実際の店舗では時と場合によって売り上げが変動し、その状況次第で発注数や人件費を抑えて経営を行っていますよね。

このように現実的な判断に近い予測結果を得たい場合、

気温や季節のような長期的な特徴と、時間帯・曜日のような短周期的特徴に加え、

天候による瞬間的なバイアス、また品質や従業員の対応といった売り上げに与える影響の大小から形状に至るまで、一様ではない誤差を含めすべて検討しなくてはいけません。

こうなってくると最終店長の勘（笑）で、単純な線形モデルではなく、基準となる線形+非線形+動的重み調整が必要となります。

モデル構築について

---

先のアイスクリームの売り上げ同様に、水質を扱う上でも同じような問題に直面します。

水質の中では水温と気温の関係が直感的に理解しやすく、モデルの中でも簡単ですが、

学術研究的な視点と実際の予測でギャップを感じます。

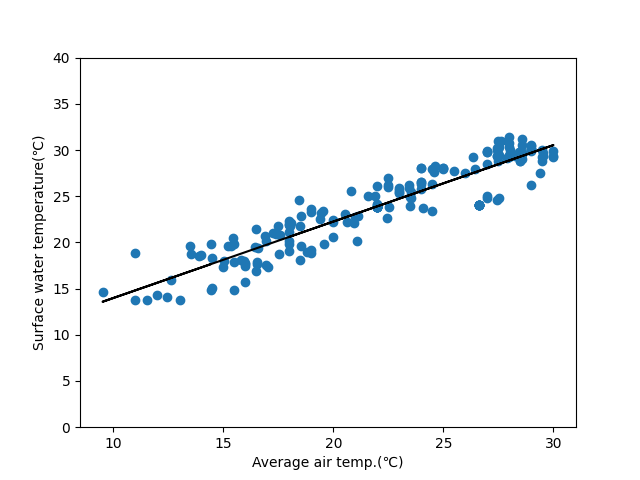
上記はある地点の過去３年の平均気温に対する表層水温です。

決定係数は0.9以上と、長期的視点では高い相関を示すことから十分予測が可能ですね。

時間周期を考慮しなくていいなら他の特徴と合わせた重回帰でも0.78そこそこの精度で予測が可能です。

では時系列だとどうでしょう。

約9日間（10min×24ｈ×9Ｄ）単位での平均気温AVE_T と水温WTを比較すると、

概ね水温＝平均気温+２℃ですが、ところどころ違う箇所があります。

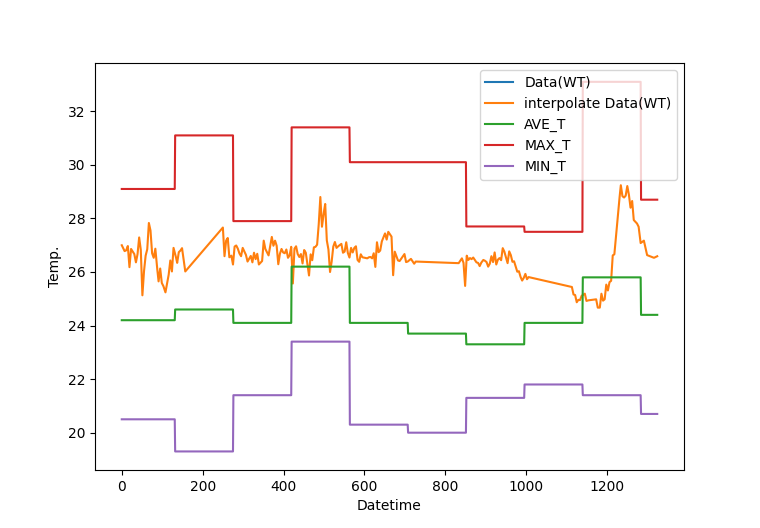
このように時間的連続性を持ったデータを線形モデルに当てはめ予測させると、

下のグラフのように平均水温を返します。

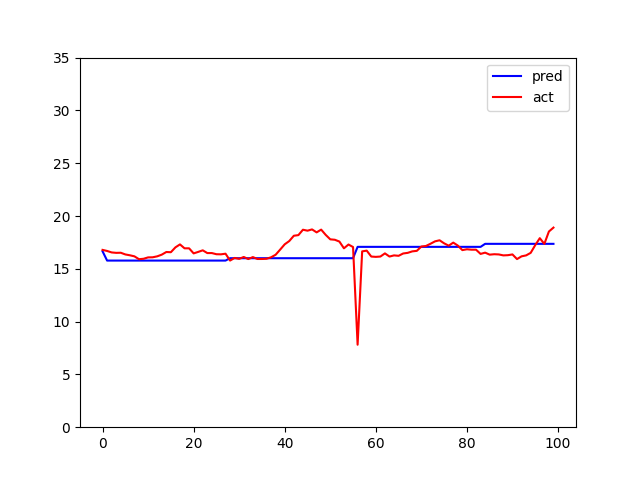
大まかには合っているので、これで十分という人もいますが、

一日単位の変化をより厳密に予測したいという場合は、さらに非線形モデルと時間依存の重み調整が必要でしょう。

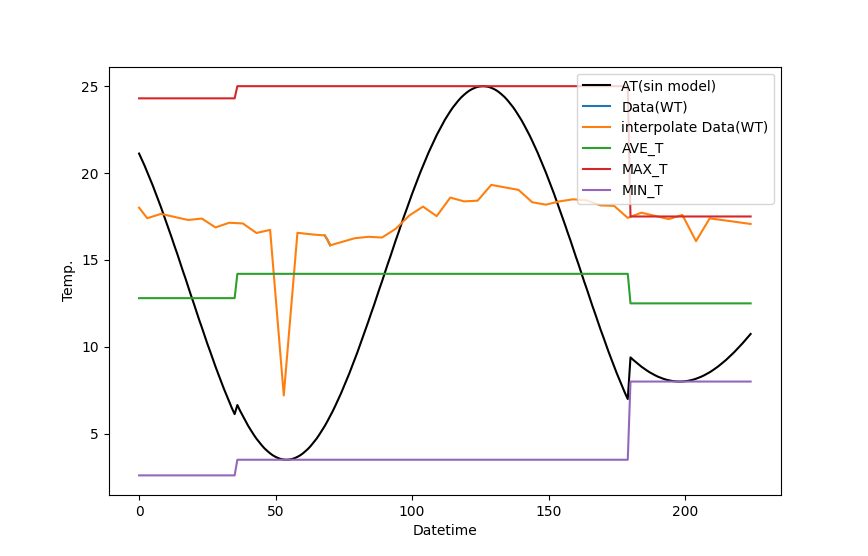
これらの結果から短期間の予測精度を高めようとすると、

相関云々よりもとにかく誤差を少なくする為にモデルのアレンジやコーディングが重要になってきます。

そもそも水温以外できれいな相関がとれる項目って、水質にはそうありません。

作為的な編集がなければ適当なモデルに放り込んでもでもうまく収束しません。悩みどころですよね。

突き詰めていくとたくさんの問題が見えてくるわけですが…いつだって理想と現実は違うものですね_(._.)_

今後も丁度よい落としどころを探して頑張ります。