みなさまこんにちは。

入門①、入門②に引き続き、今日はお待ちかね

モデルのレクチャーを行っていきます！

1. genresはジャンルごとに分離してから特徴量として使用
2. movieIdとuserId2つのカテゴライズが存在すると扱いにくいので、”mappedID”という共通IDを新たに振りなおし、これをエッジに位置づける。
3. データオブジェクトの作成
4. モデルの学習と予測

data = T.ToUndirected()(data)

transform = T.RandomLinkSplit(
    num_val=0.1,
    num_test=0.1,
    disjoint_train_ratio=0.3,
    neg_sampling_ratio=2.0,
    add_negative_train_samples=False,
    edge_types=("user", "rates", "movie"),
    rev_edge_types=("movie", "rev_rates", "user"), 
    )
train_data, val_data, test_data = transform(data)

>>> train_data
HeteroData(
  user={ node_id=[610] },#610 ：UserID=mappedIDの総数
  movie={
    node_id=[9742],　　　#9742：MovieIDの総数
    x=[9742, 20],　　　　#x   ：特徴量
  },
  (user, rates, movie)={
    edge_index=[2, 56469],
    edge_label=[24201],
    edge_label_index=[2, 24201],
  },
  (movie, rev_rates, user)={ edge_index=[2, 56469] }
)
>>> 

データオブジェクトの作成が終わり、上のスクリプトでは出来上がったデータセットを

トレーニングデータ：テストデータ：検証データ＝8：1：1に分けます。

disjoint_train_ratioはトレーニングデータの内、30％をGround truth（実際のデータに対する正解ラベル）に設定するというパラメーターです。

これまで紹介してきてた回帰、分類モデルはトレーニングデータとテストデータを8：2や7：3で分割した後、

そのままモデルに放り込めば勝手に学習してくれましたが、今回のようにノードを対象にしたデータは

近傍のノードから情報を集約し、自身のノード情報を更新する際、情報を伝播（メッセージパッシング）します。

トレーニングデータ＝個々のデータ（ノード）に対するラベル（特徴）だとすると、

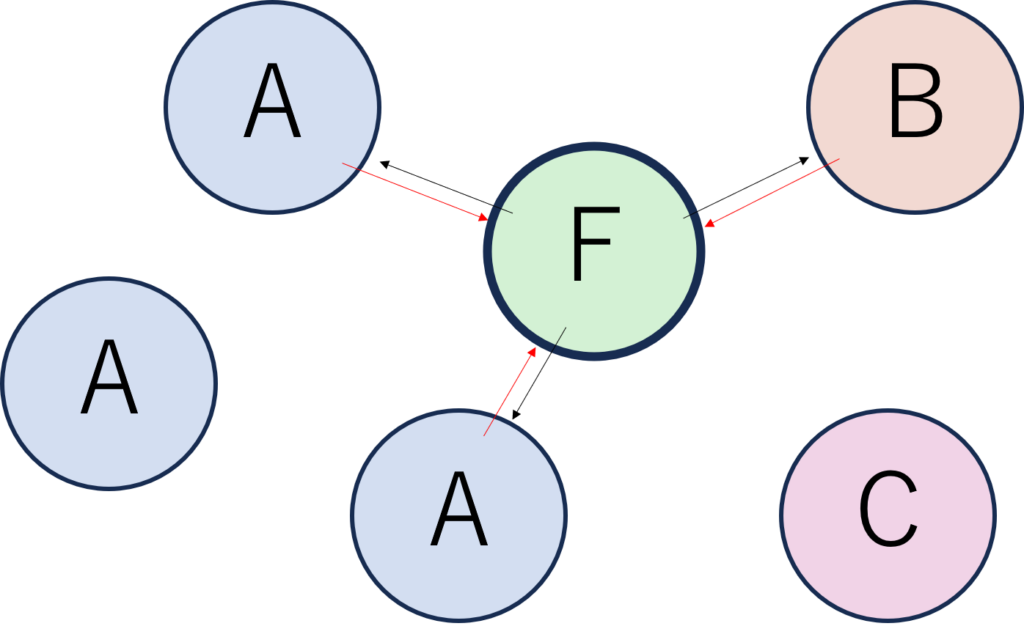
下の図で、ある緑のノード(特徴F)の近傍ノードから集約された情報（A、A、B）がＦに伝播され、

Ｆだったものが違う表現に更新されるってことだよね？（集約方法は平均、プーリング、LSTM等が選択できるようです。）

ノード情報の更新については

SAGEConvモデルの元となった文献にも以下のように記載されており、

Instead of training a distinct embedding vector for each node, we train a set of aggregator functions that learn to aggregate feature information from a node’s local neighborhood (Figure 1).
Each aggregator function aggregates information from a different number of hops, or search depth, away from a given node.(1)

近傍ノードからの情報を集約する\(K\)個の集約関数 \begin{gather} AGGREGATE_{k} , \forall k \in \{ 1,...,K\} \label{eq:1} \end{gather}

この（1）のパラメーターと重み行列\(W^{k}\)のセットを学習しているようです。

この方法は、単体ノードから特徴を学習するより精度が高く、既存の方法と比べても計算コストが少ないとのことです。

理論はニュートラルネットと似ていて、「結局何を学習しているの？」と専門家から突っ込まれそうな内容ですね（笑）

トレーニングデータの30％、Ground truthはこの学習過程で情報を集約する際、監視役として働きます。

モトハシの予想では、単体ノードの特徴分布と集約後の特徴分布とで、情報が欠損しすぎたり、過学習しないようにするため、このパラメーターが存在しているはずです。

詳しい内容は下部の引用文献をチェックしてください。

from torch_geometric.loader import LinkNeighborLoader 

edge_label_index = train_data[ "user" , "rates" , "movie" ].edge_label_index 
edge_label = train_data[ "user" , "rates" , "movie" ].edge_label 

train_loader = LinkNeighborLoader( 
    data=train_data, 
    num_neighbors=[ 20 , 10 ], 
    neg_sampling_ratio= 2.0 , 
    edge_label_index=(( "user" , "rates" , "movie" ), edge_label_index), 
    edge_label=edge_label, 
    batch_size= 128 , 
    shuffle= True , 
    )

次に、出来上がった学習用データをそのままモデルに放り込むとメモリ不足になるので

専用のデータローダーで分割します。この前処理が上記で説明した近傍サンプリングです。

LinkNeighborLoaderは入力されたエッジインデックスからnum_neighbors=[ 20 , 10 ]（1回目の反復で各ノードの近傍20個をサンプリングし、2日目の反復で10個をサンプリング）でサンプリングを行います。反復回数は2回が最も良い結果を出すそうです。

今回バッチサイズは128ですが、一般的な決め方として2のn乗で指定します。ただ、この点に関して明確な基準があるわけではなく、使うデータによってチューニングが必要だとか・・・。

from torch_geometric.nn import SAGEConv, to_hetero
import torch.nn.functional as F

♯ニューラル ネットワークの基本クラス
♯1）
class GNN(torch.nn.Module):
    def __init__(self, hidden_channels):
        super().__init__()
        self.conv1 = SAGEConv(hidden_channels, hidden_channels)
        self.conv2 = SAGEConv(hidden_channels, hidden_channels)
　　　♯順伝処理
    def forward(self, x: torch.tensor, edge_index: torch.tensor) -> torch.tensor:
　　　　　♯relu関数
        x = F.relu(self.conv1(x, edge_index))　
        x = self.conv2(x, edge_index)
        return x
♯2）
class Classifier(torch.nn.Module):
    def forward(self, x_user: torch.tensor, x_movie: torch.tensor, edge_label_index: torch.tensor) -> torch.tensor:
        # Convert node embeddings to edge-level representations:
        edge_feat_user = x_user[edge_label_index[0]]
        edge_feat_movie = x_movie[edge_label_index[1]]
        # Apply dot-product to get a prediction per supervision edge:
        return (edge_feat_user * edge_feat_movie).sum(dim=-1)
♯3）
class Model(torch.nn.Module):
    def __init__(self, hidden_channels):
        super().__init__()
        # Since the dataset does not come with rich features, we also learn two
        # embedding matrices for users and movies:
        self.movie_lin = torch.nn.Linear(20, hidden_channels)
        self.user_emb = torch.nn.Embedding(data["user"].num_nodes, hidden_channels)
        self.movie_emb = torch.nn.Embedding(data["movie"].num_nodes, hidden_channels)
        # Instantiate homogeneous GNN:
        self.gnn = GNN(hidden_channels)
        # Convert GNN model into a heterogeneous variant:
        self.gnn = to_hetero(self.gnn, metadata=data.metadata())
        self.classifier = Classifier()
    def forward(self, data: HeteroData) -> torch.tensor:
        x_dict = {
          "user": self.user_emb(data["user"].node_id),
          "movie": self.movie_lin(data["movie"].x) + self.movie_emb(data["movie"].node_id),
        } 
        # `x_dict` holds feature matrices of all node types
        # `edge_index_dict` holds all edge indices of all edge types
        x_dict = self.gnn(x_dict, data.edge_index_dict)
        pred = self.classifier(
            x_dict["user"],
            x_dict["movie"],
            data["user", "rates", "movie"].edge_label_index,
        )
        return pred
        
model = Model(hidden_channels=64)

import tqdm
import torch.nn.functional as F

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f"Device: '{device}'")
model = model.to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

for epoch in range(1, 6):
    total_loss = total_examples = 0
    for sampled_data in tqdm.tqdm(train_loader):
        optimizer.zero_grad()
        sampled_data.to(device)
        pred = model(sampled_data)
        ground_truth = sampled_data["user", "rates", "movie"].edge_label
        loss = F.binary_cross_entropy_with_logits(pred, ground_truth)
        loss.backward()
        optimizer.step()
        total_loss += float(loss) * pred.numel()
        total_examples += pred.numel()
    print(f"Epoch: {epoch:03d}, Loss: {total_loss / total_examples:.4f}")

次にモデル学習を行います。

はい、癖ツヨです(-_-メ)　序盤から3つもモデルが並んでいます。

一番基本となるモデルに組み込まれているforward関数ですが、この記述がよく分からなかったので調べたところ、入力層から出力層までの順伝にかかわる処理をしているとのことです。（※詳しくはこの記事が参考になります。）

• モデル1）：userID,movieID,エッジの間で伝達を可能にするためのモデル
• モデル2）：ノードの埋め込みとドット積の計算
• モデル3）：ノードサイズに入出力サイズ（ベクトル？）を埋め込む、モデル1）、2）の引数となるデータセットの作成と代入

※埋め込みに使われるEmbeddingについて何の話や？となる方、ここに記載がありました。

とりあえずこの３つをひっくるめて１つのモデルが完成するようです。

自分で0から作るとなると確実に骨折れそうですね(-_-;)　

せっかくなのでモデルに使われている変数の中身を少し紹介しておきます

>>> user_emb = torch.nn.Embedding(data["user"].num_nodes, hidden_channels)
>>> user_emb
Embedding(610, 64)
>>> movie_emb = torch.nn.Embedding(data["movie"].num_nodes, hidden_channels)
>>> movie_emb
Embedding(9742, 64)

>>> user_emb(data["user"].node_id),
(tensor([[ 0.5221, -0.0357,  0.7757,  ...,  0.0075, -1.2463,  0.1134],
        [ 0.0051,  1.0125,  1.7104,  ..., -0.1227,  0.8610, -2.2986],
        [-0.5411, -0.5889,  0.6766,  ..., -3.2110,  0.4981, -0.8105],
        ...,
        [-0.2703,  0.8777, -0.3048,  ..., -1.2956,  0.7249,  0.3232],
        [ 0.1480,  0.3988, -0.9881,  ...,  0.2090, -1.5912, -0.8252],
        [ 0.3176, -1.6870,  0.6174,  ...,  0.6303, -0.9793, -1.0587]],
       grad_fn=<EmbeddingBackward0>),)

>>> movie_lin(data["movie"].x) + movie_emb(data["movie"].node_id),
(tensor([[-1.4252, -0.8167,  0.1873,  ..., -0.5431, -0.4914,  0.7061],
        [-0.3358, -1.0418,  0.7100,  ..., -1.3266, -0.6093,  0.1570],
        [ 0.1819, -2.5881,  1.5484,  ...,  0.6074, -0.9182, -0.2584],
        ...,
        [-0.5166, -0.1185,  0.1338,  ..., -0.4014, -1.0112, -0.8508],
        [ 1.0847, -0.6273,  1.7170,  ..., -0.0321,  0.3118, -0.0194],
        [ 0.0313, -0.6440, -1.2957,  ...,  1.3249,  0.3862,  0.1514]],
       grad_fn=<AddBackward0>),)

数字ばっかり（笑）

最後に、バッチサイズ128のデータを５回学習し終えると同時にプロジェクトのリセットがかかりましたが（メモリ足りてるか心配になります。）、何度か初めからやり直すことでパスできました。

モデルの評価部分については説明を省きますが、今回の学習で精度は0.9286という結果になりました。

考えた人偉大だな～と感心しますね。

そんなこんなで、今回初めてグラフニュートラルネットを触ってみた感想は

• 論文の原理を理解する事
• 実質モデルの構築しないといけない
• データ操作の多さ　

この3つが相まって疲れました_(._.)_

以上！

【引用文献】

（1）William L. Hamilton，Rex Ying，Jure Leskovec，”Inductive Representation Learning on Large Graphs”，31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA.