蛇使いな彼女BLOG
【第107回】気象データの利用~方位角度とベクトル変換について~
2024.06.21

今日は前回スクレイピングで取得した気象データを利用して、風向をベクトルで示すときのコツを簡単に追記しておきます。
そもそもこの操作はかなり用途が限られてきますが、以前流向流速計のデータを図化したとき、matplotlib のquiverの癖やベクトル換算式をご紹介したと思います。当時の記事だと流向ベクトルに流速分の大きさが掛かっているので、図のようにx軸とy軸の比率が1:1ではありません。
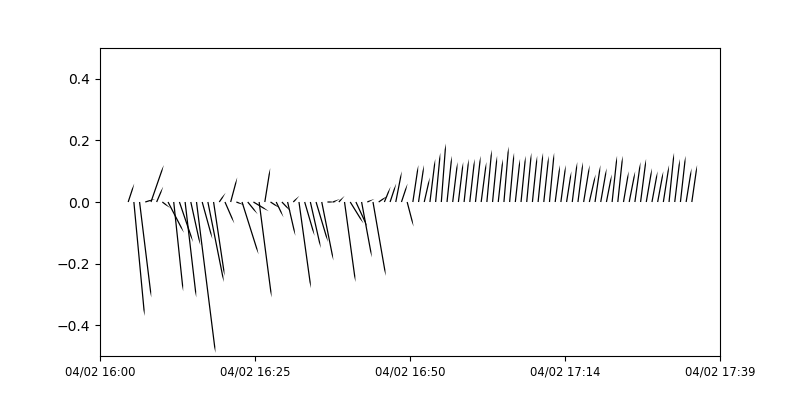
また、x軸はタイムスタンプで一定の間隔を刻んでいることから東-西、西-東の流向の見づらさと、流速が表現できない欠点も含んでいました。
今日の記事は、全てのベクトルの長さを統一した状態で、風向だけ綺麗に表現するにはどうすれば良いのかご紹介していこうと思います。
データは画像G列の平均風向(°)を例とします。
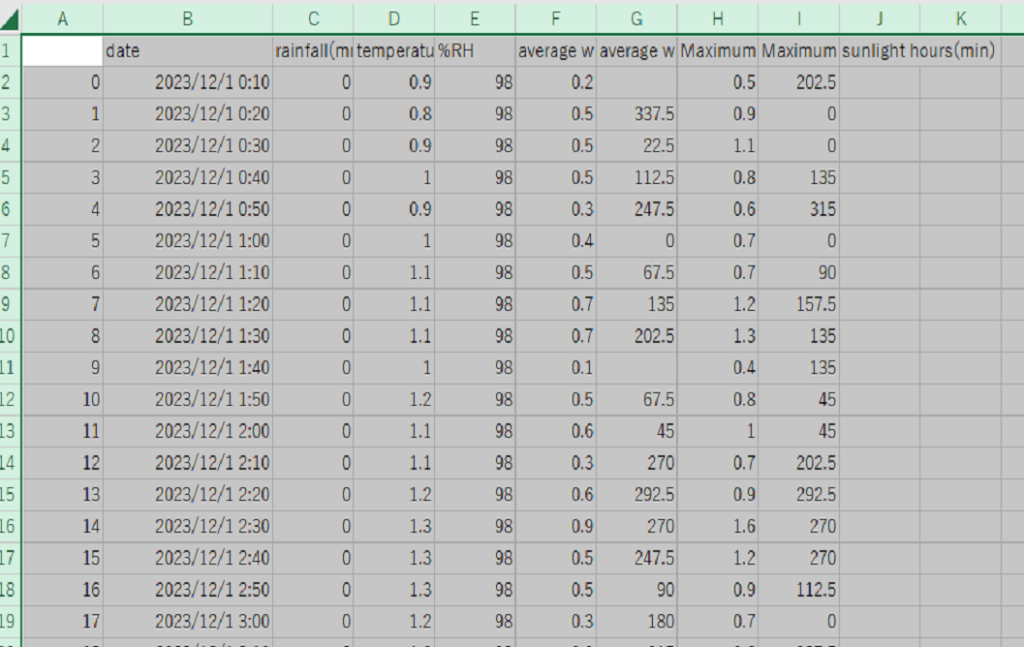
風向の値は方位で言うと北を0°として時計回りに360°で表していて、欠測部分は「静穏」となっています。またこの方位角度の表現自体は流向流速計と同じなので、風(流れ)が吹いてくる方向を示しています。ベクトルで表すときは始点に当たる位置が上の表で示されていることになるので、図化する際は角度を反転させる処理が必要です。
何を言いたいかというと、quiverではベクトルの始点座標と終点座標が必要な為、方位角度の状態からベクトル表現するには、原点を中心とする円周上の点(x,y)を求める必要があります。

角度と距離がわかっていれば公式から座標を求めることが出来るので、まずは基準である北の方位から座標を算出します。三角関数の考え方では西から反時計回りに角度が増えていくので、北はθ=90°となります。このとき点P(x1,y1)は以下で表すことが出来ます。
rad=np.deg2rad(90) r=1 x=r*np.cos(rad) y=r*np.sin(rad)
>>> print('{:1.2f},{:1.2f}'.format(x,y))
0.00,1.00
このように半径=1の単位円で考えたとき、北は(0,1)に位置します。これは原点(0,0)から北へ向かうベクトルという意味ですが、風向が北(0°)の場合、北から南に吹く風を意味するのでベクトル表現では180°反転させなければいけません。
# 風向が北(0°)の場合のベクトル座標 rad=np.deg2rad(270) r=1 x=r*np.cos(rad) y=r*np.sin(rad)
>>> print('{:1.2f},{:1.2f}'.format(x,y))
-0.00,-1.00
このように最終的に図化に必要な値は、基準地点θ=270°から同一円周上を任意の角度分移動した時の座標 P(x2,y2)の配列に相当することから、sin、cosの公式で求めることが出来ます。
また、図化する上で気をつけたいポイントとしては、半径(距離)rの大きさ指定が重要となります。
一般的に上記のような問題は単位円で考えることが殆どですが、例えば下図のように30個の方位データを個数分だけx軸方向に等間隔に置いたとき、表示するx軸のレンジはy軸との交点を含む0~30で隣り合うデータとの間隔は1しかありません。
仮に半径r=を1としたとき、各ベクトルの矢印側の座標(x,y)の取り得る範囲はそれぞれ0~1となるので、場合によっては隣接するベクトルが重なってしまいます。
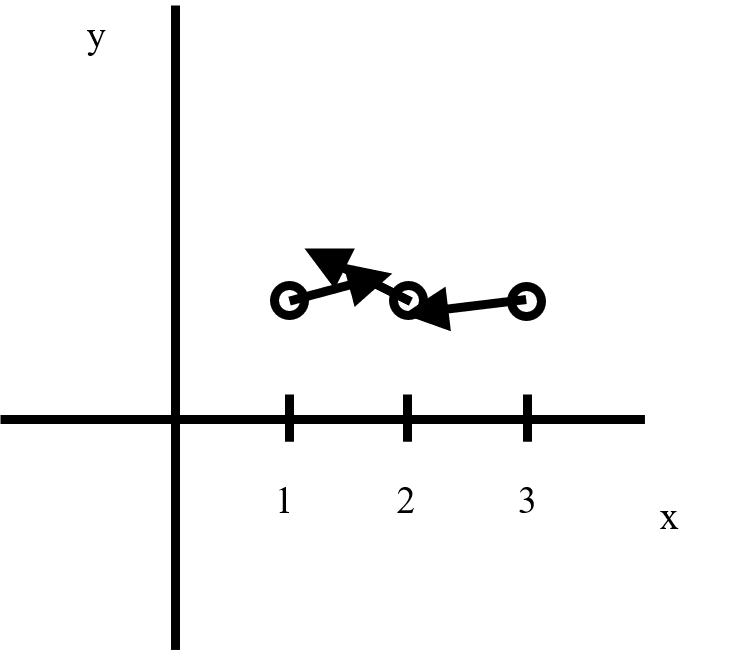
これだと見た目としては汚いですし、見づらいのでr=0.5程度にしておくのが良さそうです。
さらにモトハシはベクトルの見栄えを整えるために、始点が各ベクトルの中心となるように初期の始点と終点を結ぶ距離を2等分する点を新たな終点となるような配置に置き換えました。

では全体のコードを示します。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 気象庁データの読み込み
result=pd.read_csv('test.csv',header=0)
angle=result['average wind direction'].values
# 方位ベクトルの座標を求める
u180=np.where(angle<180)[0]
o180=np.where(angle>=180)[0]
angle[u180]=angle[u180]+180
angle[o180]=angle[o180]-180
# θ=270°のとき原点(0,0)を中心とする円周上の点(x、y)を求める
rad=np.deg2rad(270)
r=0.5
x=r*np.cos(rad)
y=r*np.sin(rad)
# 原点(0,0)、半径rの円周上の点(x、y)から任意角度回転したときの同一円周上の移動点(x_、y_)を求める
# **回転方向は反時計回りのため基準位置180°から元の角度を減算**
theta=180-angle
x_=[(x*np.cos(np.deg2rad(t)))-(y*np.sin(np.deg2rad(t))) for t in theta]
y_=[(x*np.sin(np.deg2rad(t)))+(y*np.cos(np.deg2rad(t))) for t in theta]
x_,y_=np.array(x_),np.array(y_)
# メッシュと初期原点座標の作成
X = np.linspace(0, len(theta), len(theta))
Y = np.linspace(2, 3, 1)
X, Y = np.meshgrid(X, Y)
# plot時のベクトル同士の重なりを調整
# (X,Y)(U,V)間の距離を2等分する点を終点とし、原点に対して対象な始点を求める
Bx,By=x_/2,y_/2
# 始点座標
X[0]=X[0]-Bx
Y[0]=Y[0]-By
# 終点座標
U =np.empty((X.shape[0],X.shape[1]))
V=np.empty((Y.shape[0],Y.shape[1]))
U[:,:]=np.nan
V[:,:]=np.nan
U[0]=x_
V[0]=y_
# 先頭から100までの平均風向を10個間隔でプロット
for n in range(10,110,10):
fig,ax = plt.subplots(figsize=(5,5))
ax.quiver(X[:,n-10:n], Y[:,n-10:n], U[:,n-10:n], V[:,n-10:n], angles='xy',scale_units='xy', scale=1, width=.002,headwidth=3)
ax.set(xlim=(n-10, n), ylim=(-5,5))
fig.savefig('fig{}.png'.format(n))
plt.close('all')
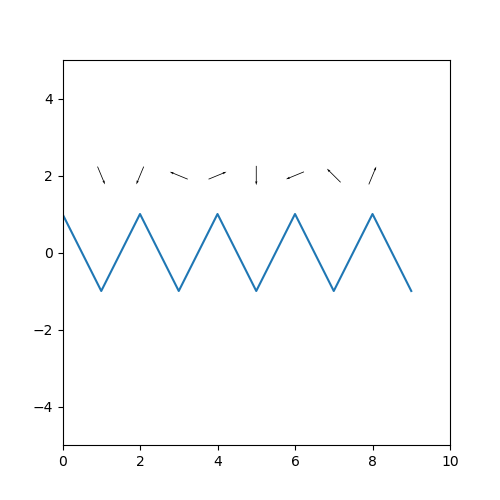
ベクトルを表示する高さなど細かく調整している分、行数は多くなっていますが、出力されたグラフは満足のいくものになりました😊
【fig10.png/fig20.png】

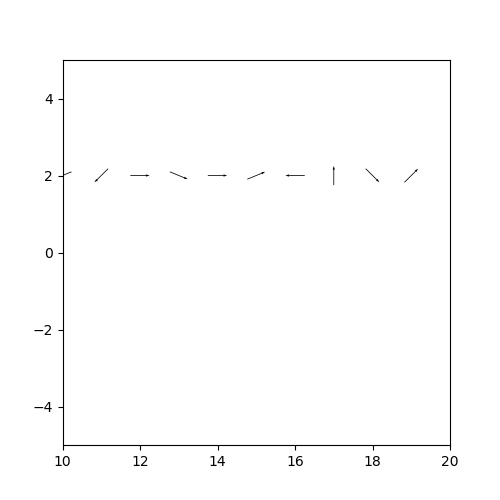
グラフではx軸の両側が見切れてしまっていますが、肝心のベクトルは重なる事なく表示できています★
メッシュのY部分を上手く調整することで、例えば風速や他の系列と組み合わせたイメージも作成可能になりますね!
では今回はここまで~

 06-6657-5130
06-6657-5130 sales@hydrolab.co.jp
sales@hydrolab.co.jp