皆様こんにちは。
最近スーパーに買い物に行った際、店内入り口に「4個で298円！」「4個購入したらクマの風船と塗り絵(箱型)プレゼント」などと、小さいクマがトレードマークの細長いパッケージのお菓子(笑)が売り出されていたので、(たまにはこういうのもいいか…と)食べたい味を4個選んで、塗り絵が描かれた専用のボックスに詰めて、その他食材と共にレジでお金を払って購入したのですが…。
重い食材から順に買い物袋に詰める癖で、お菓子の入ったボックスごとレジ横によけっちゃったままスーパー忘れてきました。
(風船だけは子供が持って帰ってきてた)
その前日にもシャンプーとコンディショナー買ったはずが、詰替えの封切ってから2つともコンディショナーという事実に気づきました。

コンディショナーの件はまだ良いとして、スーパーに忘れたお菓子はバイトの子が持って帰るのか、また店頭に並ぶのか…？と考えるとめっちゃショックでした…＿|￣|○ il||li

以上、少し傷ついた話でした(._.)笑

---

さて年内はダム関係のデータの解析やらセンサー交換時に出る誤差補正やらをメインに仕事を進めながら、今は機械的混合強度+密度から発生する鉛直混合による水の動きをどうやって定式化し、プログラム化するかということを勉強しながら考えています。
水の中で実際に起きている現象を定量化して考える第一歩として、「ブラント・ヴァイサラ振動数」という成層強度を表す指標について調べてみました。

Brunt-Vaisala frequency(ブラント・ヴァイサラ振動数)は 私達の間では浮力周波数とも呼ばれています。
水質や気象分野でよく使われていて結構有名らしいですが、数学物理が特に苦手な私は今まで手を付けずにいました(笑)。
この度は一念発起して関連文献などいろいろ調べたので、その内容についてお話したいと思います。

1．まず、浮力とは何か？

浮力とは水圧の違いで生じるものとして説明されます。
水圧P=ρgｚ(またはP=大気圧ρ0+ρgｚ)
ρ：水の密度、g：重力加速度、z：水面までの距離
浮力；N=ρVg
V:物体の体積

高校物理など一般的にはこのように水中に物体を沈めたときの上面と底面に働く圧力の違いを浮力として計算することが多く、公式にも体積Vが定義されています。
しかし、私達の言う浮力周波数の「浮力」とは水温躍層の強度として定義する浮力なので、物体を沈めたりしませんし、ここでは風や降水による流入、また外的撹乱のない(一切動きのない)安定した成層環境下で密度勾配に掛かる鉛直運動を浮力としています。

そもそも水などの液体は、気体に比べると温度上昇や圧力によって体積や密度が変化しづらいという特徴を持っています。
なので、基本的には計算上圧力も体積も省いて簡略化できるようですよ！すごいですね！
流体力学や対流分野の基礎において、このように圧力を無視して解析しやすいように近似する手法をブシネスク近似と呼ぶみたいです。

海洋では圧力によって密度が変化しないという前提で、ブシネスク近似の考え方に基づいて基準となる静止場の成層状態からの密度勾配のズレを浮力と定義しているらしいです。
(似た考え方として、流体力学的には水塊が移動したとき周囲の流体圧力が多少変化するのを無視するという定義で、パーセル法？とも呼ばれるみたいですよ。)

このような背景から、圧力を無視した条件下の運動方程式から導き出された指標が浮力周波数であり、この指標は成層化し安定した水域の、水温躍層内のある深度における密度ρ0の水塊が断熱的に上層側に運ばれるとき、持ち上げられた水が周囲水ρ1より冷たければ(密度が大きければ)重力により沈み、元の位置より下層側に沈めば再び浮上するときの振動を表しています。

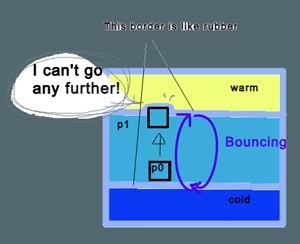
↑妙に雑でコミカルな絵で申し訳ないんですがイメージとしてはこんな感じ
(誰か簡単で使いやすいお絵かきソフトあったら教えてください(^_^;))

絵で3層に分かれているのは表層から低層にかけての水温分布(水温躍層)を表しているのではなく、躍層化した内部(淡水湖だと仮に表層から1ｍ～深度3-5ｍくらいの断面図でしょうか)の温度分布と思ってください。

水温躍層の内部は上から下まで全て同じ温度というわけではなく、大気と水面との境界から深度が1cm～3cm下がるに従い約0.01℃以下～0.05℃単位で変化しています。
場所や季節にもよりますがモトハシが見ているかぎり4月で深度3ｍ地点と表層とで約1℃ほどの違いがあります。
この場合密度ρ0の水がある高さまで持ち上げられたとき自分より温かく、密度の軽い水ρ1が周囲にあると、一度持ち上げられた水は下に落ちていきます。
逆に、自分より冷たく密度の重い水が周囲にあると浮きますね。このときの上下振動を浮力周波(ブラントヴァイサラ振動)と呼びます。

ブラントヴァイサラの角振動数Nは

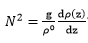
で表され、振動周期は2π/Nで計算されます。この単位は1秒(2π)間の振動回数と同じ意味を持ちます。
そうなると時間あたりのサイン波で応用したり、図化して表現できる気がしますが…
これ以上話すと私がついていけなくなるので以下省略します(^o^)

今説明したことは水温もしくは密度の差をすごく細かいところで見ていて、そうだなあ～…水分子を想像したらわかりやすいかな？
定義としては、

もし成層の境界を壊す形で矯正的に対流を起こした場合は、この周波数はあてにならない

という解釈になりますが、成層化している状況でも上下の密度差は存在するわけですから、深さの勾配としては数cm単位の話をしていることになりますね(笑)

現場の状況を表そうと思うと何を指しているのかよくわからないというのが本音です(；・∀・)
水質って難しい……

では今回はここまでとします。